3. Controllers & Dynamic Optimization

Written on June, 2025 by Bolton Tran

This post in under construction.

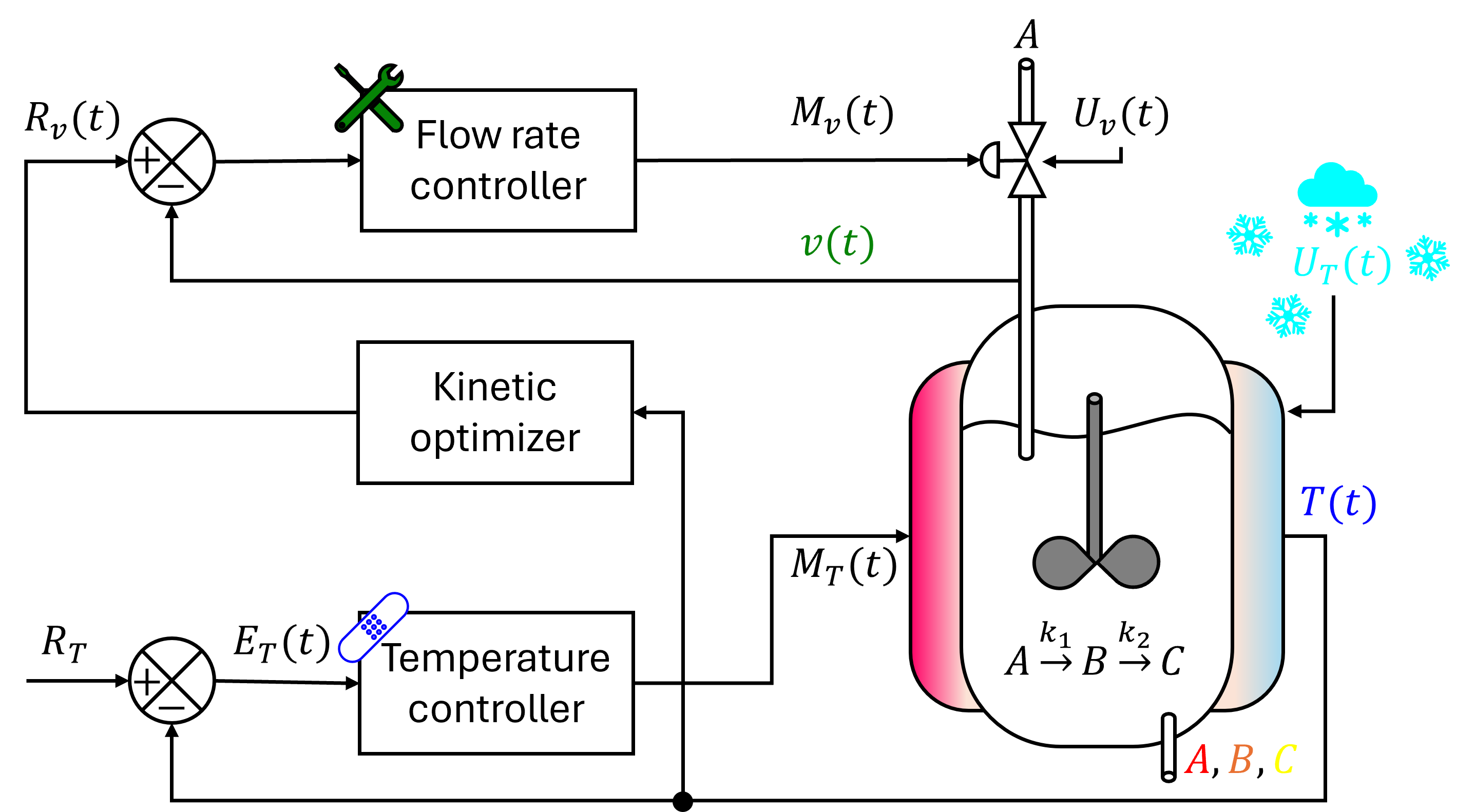
Plant settings:

1) A reaction in series is taking place in an ideal Continuous Stirred Tank Reactor (CSTR): $A \overset{k_1}{\rightarrow} B \overset{k_2}{\rightarrow} C$. The desired product $B$, of which concentration we want to maximize.

2) The reaction is endothermic, so we need to continuously heat the reactor to a constant temperature $T$.

3) The heater is “faulty”: at very cold ambient temperature ($U_T$), the controller gain drops by 90%.

4) A kinetic optimizer solves for the required volumetric flow rate $v$ of reactant $A$ so that product $B$ is continually maximized when the heater fails and reactor temperature drops.

Scenario A: No temperature drops. System operates per usual. Concentration of $B$ is maxmized as desired.

Scenario B: A WINTER STORM IS HERE!!! The temperature drops by 40 degrees over 2 days. Heater fails after a day. No correction to flow rate. Concentration of $B$ falls below desired.

Scenario C: Temperature drops and heater fails as above. Flow rate setpoints are dynamically adjusted through the kinetic optimizer. Concentration of $B$ stays as desired.

Python code: More explanation coming soon

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve
from scipy.integrate import solve_ivp
from scipy.interpolate import interp1d
from scipy.optimize import minimize_scalar

#Constants
kB=8.3144/1000 #kJ/mol.K
h=4.135667696E-15*96.49/3600 #kJ/mol.h
EA1=100 #kJ/mol
EA2=110 #kJ/mol
vol=20 #L
cA0=2 #M

#Optimize flowrate based on reaction kinetics
def ststB(v, T):
    #Rate constants
    k1=(kB*T/h)*np.exp(-EA1/kB/T)
    k2=(kB*T/h)*np.exp(-EA2/kB/T)
    #residence time
    tau=vol/v
    #Define ODEs
    def stst(c):
        #c is array for concentrations
        cA=c[0]; cB=c[1]; cC=c[2]
        dcAdt=cA0/tau - cA/tau - k1*cA
        dcBdt=-cB/tau + k1*cA - k2*cB
        dcCdt=-cC/tau + k2*cB
        return [dcAdt, dcBdt, dcCdt]
    #Solve st st ODE
    cs=fsolve(stst, [cA0,0,0] )
    return -cs[1] #minus change minimize to maximize
#Run optimization
temps=np.arange(250, 402, 2)
optv=[minimize_scalar(ststB, bounds=(1,20), args=(i), method='bounded').x for i in temps]
#Interpolate
vopt_temp=interp1d(temps, optv)

##-----Time setup-----
tmax=48
dt=1/60
time=np.arange(0, tmax+dt, dt)

##----- Set up temperature controller-----
tauT=5 #temp time constant
KpT=10 #proportional gain
KiT=1 #integral gain
T0=330 #intial temperature
MT0=T0
##Set point
RT=np.zeros(len(time))+T0
#Load fluctuation
UTramp=np.linspace(0,-40,len(time))
UTfluc=np.array([np.random.normal(loc=0, scale=2) for i in range(len(time))])
UT=UTfluc+UTramp
#initialize arrays
T=np.zeros(len(time)) 
ET=np.zeros(len(time)) 
MT=np.zeros(len(time))
#Initial C
T[0]=T0
#Intial E
ET[0]=RT[0]-T0 #error
EiT=ET[0]*dt #integral error
#Initial M
MT[0]=KpT*ET[0] + KiT*EiT + MT0 #PID logic with offset
#Initial derivatives
dT=(-T[0] + MT[0] + UT[0])/tauT

##----- Set up flow rate controller -----
tauv=2 
Kpv=5 #proportional gain
Kiv=1 #integral gain
v0=vopt_temp(T0) #intial 
Mv0=v0 #same manipulated variable as offset
##Set point and load
Rv_fixed=np.zeros(len(time))+v0 #set C0
Rv_opt=np.zeros(len(time))+v0
#Load fluctuation
Uv=np.array([np.random.normal(loc=0, scale=10) for i in range(len(time))])
##-----Set up numerical solver-----
#initialize arrays
v=np.zeros(len(time)) 
Ev=np.zeros(len(time))
Mv=np.zeros(len(time))
#Initial 
v[0]=v0
#Intial E
Ev[0]=Rv_fixed[0]-v0 #error
Eiv=Ev[0]*dt #integral error
#Initial M
Mv[0]=Kpv*Ev[0] + Kiv*Eiv + Mv0 #PID logic with offset
#Initial derivatives
dv=(-v[0] + Mv[0] + Uv[0])/tauv

##------Intialize reactor-------
cA=np.zeros(len(time))
cB=np.zeros(len(time))
cC=np.zeros(len(time))

cA[0]=2
cB[0]=0
cC[0]=0

k1=np.zeros(len(time))
k2=np.zeros(len(time))

k1[0]=(kB*T[0]/h)*np.exp(-EA1/kB/T[0])
k2[0]=(kB*T[0]/h)*np.exp(-EA2/kB/T[0])

tauR = vol/v[0]
dcA=cA0/tauR - cA[0]/tauR - k1[0]*cA[0]
dcB=-cB[0]/tauR + k1[0]*cA[0] - k2[0]*cB[0]
dcC=-cC[0]/tauR + k2[0]*cB[0]

##-----Solve=propagrate through time-----
for t in range(1,len(time)):
    #Solve temperature controller logic   
    T[t]=T[t-1]+dT*dt 
    ET[t]=RT[t]-T[t] #error
    EiT+=ET[t]*dt #cumulate integral error
    #Constrain controller gain based on load
    if UT[t]>-20:
        KpT=10 #proportional gain
        KiT=1 #integral gain
    else:
        KpT=10/10 #proportional gain
        KiT=1/10 #integral gain
    MT[t]=KpT*ET[t] + KiT*EiT + MT0 #PI logic with offset
    dT=(-T[t] + MT[t] + UT[t])/tauT

    #Solve flowrate controller logic
    v[t]=v[t-1]+dv*dt #update from previous step
    #Ev[t]=Rv_fixed[t]-v[t] #error based on fixed setpoint
    Rv_opt[t]=vopt_temp(T[t])
    Ev[t]=Rv_opt[t]-v[t] #error based on dynamic setpoint
    Eiv+=Ev[t]*dt #cumulate integral error
    Mv[t]=Kpv*Ev[t] + Kiv*Eiv + Mv0 #PI logic with offset
    dv=(-v[t] + Mv[t] + Uv[t])/tauv

    #Solve reactor kinetic
    cA[t]=cA[t-1]+dcA*dt #update from previous step
    cB[t]=cB[t-1]+dcB*dt
    cC[t]=cC[t-1]+dcC*dt
    k1[t]=(kB*T[t]/h)*np.exp(-EA1/kB/T[t])
    k2[t]=(kB*T[t]/h)*np.exp(-EA2/kB/T[t])
    tauR = vol/v[t]
    dcA=cA0/tauR - cA[t]/tauR - k1[t]*cA[t]
    dcB=-cB[t]/tauR + k1[t]*cA[t] - k2[t]*cB[t]
    dcC=-cC[t]/tauR + k2[t]*cB[t]
#----Plot-----
fig, axes=plt.subplots(1,4, figsize=(10,2),dpi=300)

axes[0].plot(time, UT+RT, c='cyan')
axes[0].set_ylim(250, 350)
axes[0].set_ylabel(r'$U_T + R_T$ (K)', fontsize=12)

axes[1].plot(time, T, c='b')
axes[1].plot(time, RT, ls=':', c='k')
axes[1].set_ylim(310, 350)
axes[1].set_ylabel(r'$T$ (K)', fontsize=12)

axes[2].plot(time, v, c='g')
#axes[2].plot(time, Rv_fixed, ls='--',c='k')
axes[2].plot(time, Rv_opt, ls=':',c='k')
axes[2].set_ylim(2, 14)
axes[2].set_ylabel(r'$v$ (L/hr)', fontsize=12)

cABC=[cA, cB, cC]
colors=['r', 'orange', 'yellow']
[axes[3].plot(time, cABC[i], c=colors[i]) for i in range(3)]
axes[3].set_ylabel(r'$c$ (mol/L)', fontsize=12)
axes[3].annotate(r'$c_A$', xy=(10, 0.4), color='r', fontsize=12)
axes[3].annotate(r'$c_B$', xy=(10, 1.6), color='orange', fontsize=12)
axes[3].annotate(r'$c_C$', xy=(10, 0.01), color='yellow', fontsize=12)

[i.set_xlim(0,48) for i in axes]
[i.set_xlabel('Time (hr)', fontsize=12) for i in axes]
[i.tick_params(labelsize=12) for i in axes]
plt.tight_layout()
plt.show()